ANALISIS RANGKAIAN AC - TEOREMA RANGKAIAN

Teorema Superposisi

A. Pengertian

Arus atau tegangan yang melalui sebuah elemen dalam sebuah jaringan linear dua arah yang memiliki beberapa sumber sama dengan jumlah aljabar arus atau tegangan yang dihasilkan secara terpisah oleh masing-masing sumber.

Teorema superposisi berlaku untuk semua rangkaian linear dan bilateral. Dalam teorema superposisi ini terdapat dua atau lebih sumber yang bebas. Sumber tersebut bisa tegangan dengan tegangan dan bisa tegangan dengan arus. Sumber-sumber tersebut tidak dapat bekerja secara bersamaan atau hanya berpatokan pada satu sumber saja. Sumber-sumber ini bekerja satu persatu. Sumber-sumber tegangan yang akan di tahan sewaktu salah satu sumber lain (sumber tunggal) bekerja digantikan oleh rangkaian hubung singkat (short), sumber-sumber arus digantikan dengan rangkaian terbuka (o.c). Teorema superposisi digunakan untuk menghitung besar arus pada masing-masing beban dengan menentukan terlebih dahulu arah arus pada rangkaian. Dibawah ini adalah contoh gambar rangkaian listrik yang dapat di analisis dengan metode atau teorema superposisi.

B. Sifat- Sifat Teorema Superposisi

1. Berpatokan pada satu sumber, sumber (E) yang lain di hubung singkat (short) atau jika pada arus (I) dalam rangkaian terbuka (o.c)

2. Tidak berpengaruh dengan sumbernya

3. Besar I₃ akan sama dengan (gambar a) apabila searah

(Gambar a)

4. Jika (Gambar b) atau sebaliknya

(Gambar b)

C. Langkah-langkah Analisa Teorema Superposisi

a. Menghitung arus dengan dua sumber tegangan.

1. Berpatokan pada V₁dan pada V₂di short.

· Cari arus yang dihasilkan oleh V₁ saja. Ganti sumber tegangan V₂ dengan hubung singkat.

_·Carilah arus pada I₁¹ dengan menggantikan R_1,R₂dan R₃menjadi R₄

· Setelah R_T di ketahui maka I₁¹, I₂¹, I₃¹ dapat di cari

2. Bepatokan pada V₂saja dan pada V₁di short

· Cari arus yang dihasilkan oleh V₂ saja. Ganti sumber tegangan V₁ dengan hubung singkat.

_·Carilah arus pada I₁² dengan menggantikan R_1,R₂dan R₃menjadi R₅

· Setelah R_T di ketahui maka I₁², I₂², I₃² dapat di cari dengan formula dibawah ini:

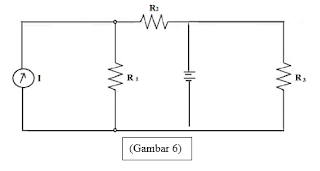
b. Menghitung arus menggunakan sumber tegangan dan arus.

1. Berpatokan pada I dan E di hubung singkat

· Cari arus yang dihasilkan oleh I saja.

· Ganti sumber tegangan E dengan hubung singkat. (Lihat gambar di bawah ini)

2. Berpatokan pada sumber tegangan (E)

· Cari arus yang dihasilkan oleh tegangan E saja.

· Ganti arus I dengan rangkaian terbuka (o.c)

SOAL DAN JAWABAN

1. Carilah arus yang melewati rangkaian dibawah ini

A. Berpatokan pada I dan E di hubung singkat (short)

B. Berpatokan pada E dan I dalam rangkaian terbuka (o.c)

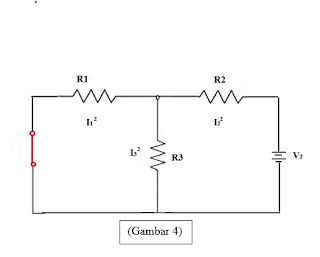
2. Carilah arus yang melalui rangkaian dibawah ini

Jawab:

A. Berpatokan pada E₁dan E₂di hubung singkat (short)

· Setelah R_T di ketahui maka I₁¹, I₂¹, I₃¹ dapat di cari

B. Berpatokan pada E₂dan E₁di hubung singkat (short)

· Setelah R_T di ketahui maka I₁¹, I₂¹, I₃¹ dapat di cari

Torema Substitusi

Pada teorema ini berlaku bahwa :

Suatu komponen atau elemen pasif yang dilalui oleh sebuah arus yang mengalir (sebesar i) maka pada komponen pasif tersebut dapat digantikan dengan sumber tegangan V_s yang mempunyai nilai yang sama saat arus tersebut melalui komponen pasif tersebut.

Jika pada komponen pasifnya adalah sebuah resistor sebesar R, maka sumber tegangan penggantinya bernilai V_s = i.R dengan tahanan dalam dari sumber tegangan tersebut samadengan nol.

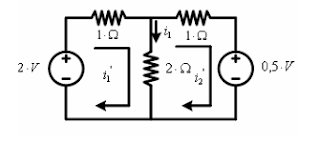
Contoh Latihan:

dengan teorema substitusi :

Resistor 1  yang dilalui arus i₂ sebesar 0,5 A, jika diganti dengan V_s = 1.i₂ = 0,5 V, akan menghasilkan arus i₁ yang sama pada saat sebelum dan sesudah diganti dengan sumber tegangan.

Teorema Thevenin

Pada teorema ini berlaku bahwa :

Suatu rangkaian listrik dapat disederhanakan dengan hanya terdiri dari satu buah sumber tegangan yang dihubungserikan dengan sebuah tahanan ekivelennya pada dua terminal yang diamati.

Tujuan sebenarnya dari teorema ini adalah untuk menyederhanakan analisis rangkaian, yaitu membuat rangkaian pengganti yang berupa sumber tegangan yang dihubungkan seri dengan suatu resistansi ekivalennya.

Pada gambar diatas, dengan terorema substitusi kita dapat melihat rangkaian sirkit B dapat diganti dengan sumber tegangan yang bernilai sama saat arus melewati sirkit B pada dua terminal yang kita amati yaitu terminal a-b.

Setelah kita dapatkan rangkaian substitusinya, maka dengan menggunakan teorema superposisi didapatkan bahwa :

1. Ketika sumber tegangan V aktif/bekerja maka rangkaian pada sirkit linier A tidak aktif (semua sumber bebasnya mati diganti tahanan dalamnya), sehingga didapatkan nilai resistansi ekivelnnya.

2. Ketika sirkit linier A aktif/bekerja maka pada sumber tegangan bebas diganti dengan tahanan dalamnya yaitu nol atau rangkaian short circuit.

Dengan menggabungkan kedua keadaan tadi (teorema superposisi) maka didapatkan :

Pada saat terminal a-b di open circuit (OC), maka i yang mengalir samadengan nol (i = 0), sehingga :

Cara memperoleh resistansi penggantinya (R_th) adalah dengan mematikan atau menon aktifkan semua sumber bebas pada rangkaian linier A (untuk sumber tegangan tahanan dalamnya = 0 atau rangkaian short circuit dan untuk sumber arus tahanan dalamnya = ¥ atau rangkaian open circuit).

Jika pada rangkaian tersebut terdapat sumber dependent atau sumber tak bebasnya, maka untuk memperoleh resistansi penggantinya, terlebih dahulu kita mencari arus hubung singkat (i_sc), sehingga nilai resistansi penggantinya (R_th) didapatkan dari nilai tegangan pada kedua terminal tersebut yang di-open circuit dibagi dengan arus pada kedua terminal tersebut yang di- short circuit .

Langkah-langkah penyelesaian dengan teorema Thevenin :

1. Cari dan tentukan titik terminal a-b dimana parameter yang ditanyakan.

2. Lepaskan komponen pada titik a-b tersebut, open circuit kan pada terminal a-b kemudian hitung nilai tegangan dititik a-b tersebut (V_ab = V_th).

3. Jika semua sumbernya adalah sumber bebas, maka tentukan nilai tahanan diukur pada titik a-b tersebut saat semua sumber di non aktifkan dengan cara diganti dengan tahanan dalamnya (untuk sumber tegangan bebas diganti rangkaian short circuit dan untuk sumber arus bebas diganti dengan rangkaian open circuit)

(R_ab = R_th).

4. Jika terdapat sumber tak bebas, maka untuk mencari nilai tahanan pengganti

Theveninnya didapatkan dengan cara

5. Untuk mencari Isc pada terminal titik a-b tersebut dihubungsingkatkan dan dicari arus yang mengalir pada titik tersebut (I_ab = I_sc).

6. Gambarkan kembali rangkaian pengganti Theveninnya, kemudian pasangkan kembali komponen yang tadi dilepas dan hitung parameter yang ditanyakan.

Contoh Latihan:

untuk sumber bebas/ independent

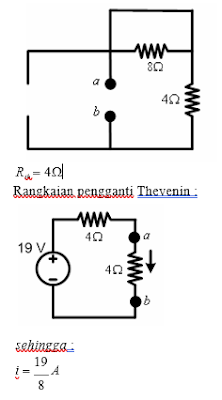
1. Tentukan nilai arus i dengan teorema Thevenin !

Jawaban:

Tentukan titik a-b pada R dimana parameter i yang ditanyakan, hitung tegangan dititik a-b pada saat terbuka :

Mencari R_th ketika semua sumber bebasnya tidak aktif (diganti dengan tahanan dalamnya) dilihat dari titik a-b :

untuk sumber tak bebas/ dependent

1. Tentukan nilai V dengan teorema Thevenin !

Jawaban:

Mencari V_ab dimana tegangan di R=3Ω, dimana rangkaian tersebut terbuka :

Vab = Voc = -2i1 - 1.i1 + 12 = -3i1 + 12 dim ana : i = -6 A

Voc = (-3x - 6) + 12 = 18 + 12 = 30V

Karena terdapat sumber tak bebas, maka untuk mencari R_th tidak bisa langsung dengan mematikan semua sumbernya, sehingga harus dicari nilai I_sc :

Teorema Norton

Pada teorema ini berlaku bahwa :

Suatu rangkaian listrik dapat disederhanakan dengan hanya terdiri dari satu buah sumber arus yang dihubungparalelkan dengan sebuah tahanan ekivelennya pada dua terminal yang diamati.

Tujuan untuk menyederhanakan analisis rangkaian, yaitu dengan membuat rangkaian pengganti yang berupa sumber arus yang diparalel dengan suatu tahanan ekivalennya.

Langkah-langkah penyelesaian dengan teorema Norton :

1. Cari dan tentukan titik terminal a-b dimana parameter yang ditanyakan.

2. Lepaskan komponen pada titik a-b tersebut, short circuit kan pada terminal a-b kemudian hitung nilai arus dititik a-b tersebut (I_ab = I_sc = I_N).